- Show that in a topological group, the connected component of the identity is a normal subgroup.
- Show that the action of the group
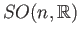 on the sphere
on the sphere  given by matrix multiplication is
transitive. You need to employ the Gram-Schmidt theorem to complete a given unit vector to an orthonormal basis.
given by matrix multiplication is
transitive. You need to employ the Gram-Schmidt theorem to complete a given unit vector to an orthonormal basis.
- Suppose a group
 acts transitively on a set
acts transitively on a set 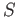 and
and 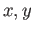 are a pair of points in
are a pair of points in 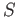 and
and 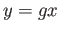 . Then
the subgroups stab
. Then
the subgroups stab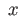 and stab
and stab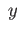 are conjugates and
are conjugates and 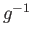 (stab
(stab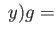 stab
stab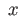 .
.
- (i)
- Show that the map
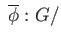 stab
stab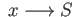 given by
given by
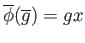 is well-defined, bijective and
is well-defined, bijective and
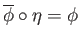 .
.
- (ii)
- Suppose that
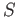 is a topological space,
is a topological space,  is a topological group and the action
is a topological group and the action
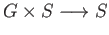 is continuous. Show that the map
is continuous. Show that the map
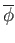 is continuous.
is continuous.
- (iii)
- Deduce that if
 is compact and
is compact and 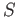 is Hausdorff then
is Hausdorff then
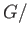 stab
stab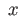 and
and 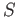 are homeomorphic.
are homeomorphic.
- Examine whether the map
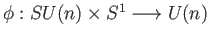 given by
given by
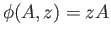 is a homeomorphism.
is a homeomorphism.
- Show that the group of all unitary matrices
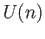 is compact and connected. Regarding
is compact and connected. Regarding 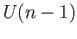 as a subgroup of
as a subgroup of 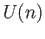 in a natural way, recognize the quotient space as a familiar space.
in a natural way, recognize the quotient space as a familiar space.
- Show that the subgroups
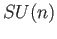 consisting of matrices in
consisting of matrices in 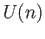 with determinant one are connected for every
with determinant one are connected for every  .
.
- Suppose
 is a topological group and
is a topological group and  is a normal subgroup, prove that
is a normal subgroup, prove that 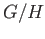 is Hausdorff if and only
if
is Hausdorff if and only
if  is closed.
is closed.
in
Lecture VI (Test - I)
in
- Prove that the intervals
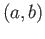 and
and 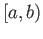 are non-homeomorphic subsets of
are non-homeomorphic subsets of
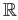 . Prove that if
. Prove that if  and
and
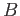 are homeomorphic subsets of
are homeomorphic subsets of
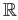 , then
, then  is open in
is open in
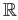 if and only if
if and only if 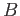 is open in
is open in
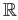 .
Is an injective continuous map
.
Is an injective continuous map
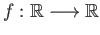 a homeomorphism onto its image?
a homeomorphism onto its image?
- Using Tietze's extension theorem or otherwise construct a continuous map from
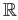 into
into
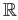 such that
the image of
such that
the image of
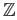 is not closed in
is not closed in
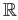 .
.
- If
 is a compact subset of a topological group
is a compact subset of a topological group  and
and 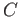 is a closed subset of
is a closed subset of  , is it true that
, is it true that 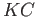 is
closed in
is
closed in  ? What if
? What if  and
and 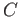 are merely closed subsets of
are merely closed subsets of  ?
?
- Removing three points from
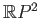 we get an open set
we get an open set  and a continuous map
and a continuous map
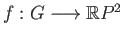 given by
given by
![$ f([x_1, x_2, x_3]) = [x_2x_3, x_3x_1, x_1x_2]$](img461.png) . Which three points
need to be removed? Prove the continuity of
. Which three points
need to be removed? Prove the continuity of  .
.
- Let
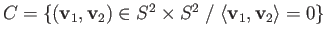 . Is
. Is 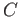 connected? Is
connected? Is 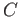 homeomorphic to
homeomorphic to
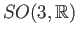 ?
?
- Prove that
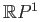 is homeomorphic to
is homeomorphic to 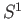 .
.
in
Lecture VII - Paths, homotopies and the fundamental group
in
In this lecture we shall introduce the most basic object in algebraic topology, the fundamental group. For this purpose
we shall define the notion of homotopy of paths in a topological space  and show that this is an equivalence relation. We then fix a point
and show that this is an equivalence relation. We then fix a point
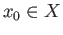 in the topological space and look at the set of all equivalence classes of
loops starting and ending at
in the topological space and look at the set of all equivalence classes of
loops starting and ending at  .
This set is then endowed with a binary operation that turns it into a group known as the fundamental group
.
This set is then endowed with a binary operation that turns it into a group known as the fundamental group
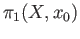 . Besides being the most basic object in algebraic topology, it is of paramount importance
in low dimensional topology. A detailed study of this group will occupy the rest of part I of this course.
However in this lecture we shall focus only on the most elementary results.
. Besides being the most basic object in algebraic topology, it is of paramount importance
in low dimensional topology. A detailed study of this group will occupy the rest of part I of this course.
However in this lecture we shall focus only on the most elementary results.
All spaces considered here are path connected Hausdorff spaces.
Subsections
nisha
2012-03-20