Proof:

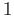We must remark that we are not assuming anything about $\phi$ besides continuity and the fact that it fixes 0 and $1$. In particular $\phi$ need not be monotone. The idea of proof is simple. The convexity of the unit square $[0, 1]\times [0, 1]$ is used to tweak the graph of $\phi$ onto the graph of the identity map of $[0, 1]$. Thus we define a continuous map $F: [0, 1]\times [0, 1] \longrightarrow X$ by the prescription

$$F(s, t) = \gamma(s\phi(t) + (1-s)t)$$

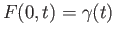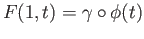Now $F(0, t) = \gamma(t)$, $F(1, t) = \gamma\circ\phi(t)$. For verifying that the end points are fixed during deformation,

$$F(s,0) = \gamma(s\phi(0)) = \gamma(0)$$

$$F(s,1) = \gamma(s\phi(1) + (1-s)) = \gamma(1), \quad 0 \leq s \leq 1.$$