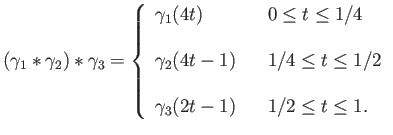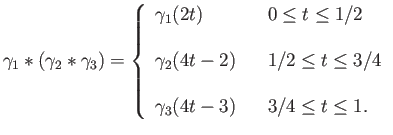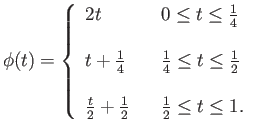Proof:

By direct calculation we get on the one hand

$$(\gamma_1 \ast \gamma_2) \ast \gamma_3 = \left\{\begin{array}{lll... ...q 1/2 \\ &&\\ \gamma_3(2t-1) & & 1/2 \leq t \leq 1. \\ \end{array} \right.$$

On the other hand, for 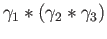$\gamma_1 \ast (\gamma_2 \ast \gamma_3)$ we find

$$\gamma_1 \ast (\gamma_2 \ast \gamma_3) = \left\{\begin{array}{lll... ...q 3/4 \\ &&\\ \gamma_3(4t-3) & & 3/4 \leq t \leq 1. \\ \end{array} \right.$$

These two are homotopic by the reparametrization theorem. To see this define $\phi:[0,1] \rightarrow [0,1]$ by

$$\phi(t) = \left\{\begin{array}{lll} 2t && 0 \leq t \leq \frac{1}{... ... \frac{t}{2}+\frac{1}{2} && \frac{1}{2} \leq t \leq 1. \\ \end{array} \right.$$

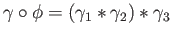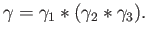one verifies that $\gamma \circ \phi = (\gamma_1 \ast \gamma_2) \ast \gamma_3$ where $\gamma = \gamma_1 \ast (\gamma_2 \ast \gamma_3).$ By theorem (7.2) the result follows.

We are now ready to define the fundamental group.