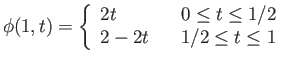One uses the reparametrization theorem to prove (ii) and (iii). Proof of (i) is more involved and we indicate two different
methods by which this can be achieved. On the boundary  of the unit square
of the unit square  we define a map
we define a map
![$ \phi: \dot{I}^2 \longrightarrow [0, 1]$](img547.png) as follows.
as follows.
Along the part  of the boundary,
of the boundary,
By Tietze's extension theorem  extends continuously to
extends continuously to 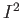 taking values in
taking values in ![$ [0, 1]$](img13.png) .
Consider now the map
.
Consider now the map
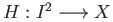 given by
given by
It is readily checked that  establishes a homotopy between
establishes a homotopy between
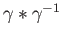 and the constant path
and the constant path
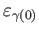 .
. 
nisha
2012-03-20