The result is false if the hypothesis of normality of  is dropped. For example consider a cube
in
is dropped. For example consider a cube
in
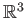 with center at the origin and
with center at the origin and  be the subgroup of
be the subgroup of
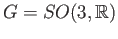 that map the cube to itself.
Then
that map the cube to itself.
Then  is the symmetric group on four letters (proof?). Clearly
is the symmetric group on four letters (proof?). Clearly  is not in the center of
is not in the center of  .
.
nisha
2012-03-20