<574>>
Lecture V - Topological Groups
in
A topological group is a topological space which is also a group such that the group operations
(multiplication and inversion) are continuous.
They arise naturally as continuous groups of symmetries of topological spaces. A case in point is the group
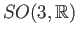 of rotations of
of rotations of
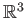 about the origin which is a group of symmetries of the sphere
about the origin which is a group of symmetries of the sphere 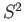 .
Many familiar examples of topological spaces are in fact topological groups. The most basic example of-course is the
real line with the group structure given by addition. Other obvious examples are
.
Many familiar examples of topological spaces are in fact topological groups. The most basic example of-course is the
real line with the group structure given by addition. Other obvious examples are
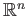 under addition, the multiplicative group of unit complex numbers
under addition, the multiplicative group of unit complex numbers 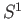 and
the multiplicative group
and
the multiplicative group
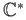 .
.
In the previous lectures we have seen that
the group
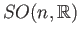 of orthogonal matrices with determinant one and the group
of orthogonal matrices with determinant one and the group 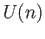 of unitary matrices
are compact.
In this lecture we initiate a systematic study of topological groups and take a
closer look at some of the matrix groups such as
of unitary matrices
are compact.
In this lecture we initiate a systematic study of topological groups and take a
closer look at some of the matrix groups such as
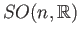 and the unitary groups
and the unitary groups 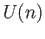 .
.
Subsections
nisha
2012-03-20
![]() of orthogonal matrices with determinant one and the group
of orthogonal matrices with determinant one and the group ![]() of unitary matrices
are compact.
In this lecture we initiate a systematic study of topological groups and take a
closer look at some of the matrix groups such as
of unitary matrices
are compact.
In this lecture we initiate a systematic study of topological groups and take a
closer look at some of the matrix groups such as
![]() and the unitary groups
and the unitary groups ![]() .
.