Since  is discrete, the identity element is not a limit point of
is discrete, the identity element is not a limit point of  and so there is a
neighborhood
and so there is a
neighborhood  of the identity such that
of the identity such that
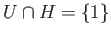 . We may assume
. We may assume  has the property that if
has the property that if
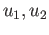 are in
are in  then the product
then the product
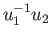 is in
is in  . This follows from the continuity of the group
operation and a detailed verification is left as an exercise.
It is easy to see that if
. This follows from the continuity of the group
operation and a detailed verification is left as an exercise.
It is easy to see that if 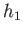 and
and 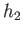 are two distinct elements of
are two distinct elements of  then
then
Fix 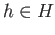 and consider now the set
and consider now the set  given by
given by
We shall show that the subgroup  contains a neighborhood of the identity. Pick a neighborhood
contains a neighborhood of the identity. Pick a neighborhood  of the
identity such that
of the
identity such that
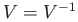 and
and
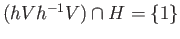 . Then for any
. Then for any  , we have on the one hand
, we have on the one hand
and on the other hand
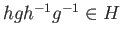 since
since  is normal.
Hence
is normal.
Hence
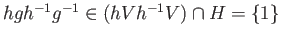 which shows that
which shows that 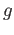 belongs to
belongs to  and
and  contains a
neighborhood of the unit element. We may now invoke the previous theorem.
contains a
neighborhood of the unit element. We may now invoke the previous theorem.  nisha
2012-03-20
nisha
2012-03-20