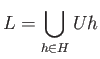Let  be the open neighborhood of the identity that is contained in
be the open neighborhood of the identity that is contained in  and
and 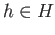 be arbitrary. Since multiplication by
be arbitrary. Since multiplication by 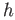 is a homeomorphism, the set
is a homeomorphism, the set
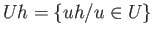 is also open and also contained in
is also open and also contained in  . Hence the set
. Hence the set
is open and contained in  . Since
. Since  contains the identity element,
contains the identity element,
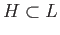 and we conclude that
and we conclude that
 is open. Our job will be over if we can show that
is open. Our job will be over if we can show that  is closed as well. Let
is closed as well. Let
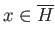 be arbitrary.
Since the neighborhood
be arbitrary.
Since the neighborhood 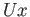 of
of 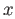 contains a point
contains a point  , there exists
, there exists 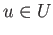 such that
such that 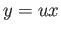 which, in
view of the fact that
which, in
view of the fact that
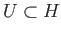 , implies
, implies 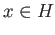 . Hence
. Hence
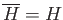 .
.

nisha
2012-03-20