Exercises

1. What happens if we omit the surjectivity hypothesis on the function 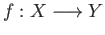$f : X \longrightarrow Y$ in the definition of quotient topology on $Y$ induced by $f$ ?
2. Show that the space obtained from the unit ball 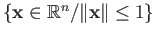$\{{\bf x}\in \mathbb{R}^n/ \Vert{\bf x}\Vert \leq 1\}$ by collapsing its boundary to a singleton, is homeomorphic to the sphere $S^n$.
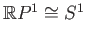3. Show that $\mathbb{R}P^1 \cong S^1$ by considering the map 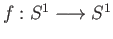$f : S^1 \longrightarrow S^1$ given by $f(z) = z^2$.
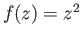4. Try to show that 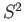$S^2$ is not homeomorphic to 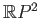$\mathbb{R}P^2$. Would the Jordan curve theorem help?
5. Show that the boundary of the Möbius band is homeomorphic to $S^1$.
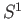6. Does a Möbius band result upon cutting the projective plane 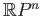$\mathbb{R}P^n$ along a closed curve on it?

#574#>