It is clear that
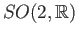 is connected (why?). Turning to the case
is connected (why?). Turning to the case 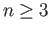 , we consider the action of
, we consider the action of
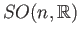 on the standard unit sphere
on the standard unit sphere  in
in
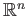 given by
given by
where
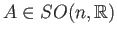 and
and
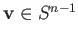 .
It is an exercise for the student to check that this group action
is transitive and that the stabilizer of the unit vector
.
It is an exercise for the student to check that this group action
is transitive and that the stabilizer of the unit vector
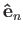 is the subgroup
is the subgroup  consisting of all those matrices in
consisting of all those matrices in
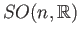 whose last column is
whose last column is
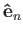 . The subgroup
. The subgroup  is
homeomorphic to
is
homeomorphic to
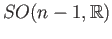 and so, by induction hypothesis, is connected.
By exercise 3, the quotient space
and so, by induction hypothesis, is connected.
By exercise 3, the quotient space
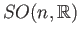 is homeomorphic to
is homeomorphic to
 which is connected.
So the theorem can be applied with
which is connected.
So the theorem can be applied with
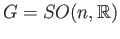 ,
,
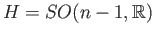 and
and 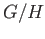 is the sphere
is the sphere
 with
with 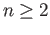 .
. 
nisha
2012-03-20