A topological group is a group which is also a topological space
such that the singleton set containing the identity element is closed and the group operation
and the inversion
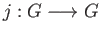 given by
given by
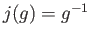 are continuous, where
are continuous, where 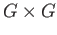 is given the product topology.
is given the product topology.
We leave it to the reader to prove that a topological group is a Hausdorff space.
It is immediate that the following maps of a topological group  are continuous:
are continuous:
- Given
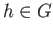 the maps
the maps
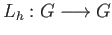 and
and
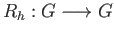 given by
given by
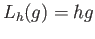 and
and
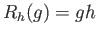 .
These are the left and right translations by
.
These are the left and right translations by 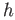 .
.
- The inner-automorphism given by
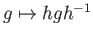 which is a homeomorphism.
which is a homeomorphism.
Note that the determinant map is a continuous group homomorphism from
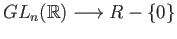 .
The image is surjective from which it follows that
.
The image is surjective from which it follows that
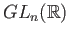 is disconnected as a topological space.
is disconnected as a topological space.
nisha
2012-03-20
![]() are continuous:
are continuous: