If  is connected then so is
is connected then so is 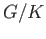 since the quotient map
since the quotient map
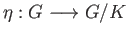 is a
continuous surjection. To prove the converse suppose that
is a
continuous surjection. To prove the converse suppose that  and
and 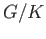 are connected and
are connected and
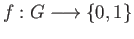 be an arbitrary continuous map. We have to show that
be an arbitrary continuous map. We have to show that  is constant.
The restriction of
is constant.
The restriction of  to
to  must be constant and since each coset
must be constant and since each coset
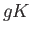 is connected,
is connected,  must be constant on
must be constant on 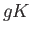 as well taking value
as well taking value 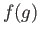 .
Thus we have a well defined map
.
Thus we have a well defined map
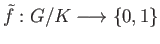 such that
such that
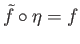 .
By the fundamental property of quotient spaces, it follows that
.
By the fundamental property of quotient spaces, it follows that 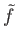 is continuous and so must be
constant since
is continuous and so must be
constant since 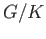 is connected. Hence
is connected. Hence  is also constant and we conclude that
is also constant and we conclude that  is connected.
is connected. 
Since we shall not need (2), we shall omit the proof. A proof is available in [12], p. 109.
nisha
2012-03-20