Let 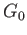 be the connected component of
be the connected component of  containing the identity and
containing the identity and
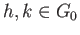 be arbitrary.
The set
be arbitrary.
The set 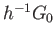 is connected and contains the identity and so
is connected and contains the identity and so
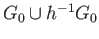 is also connected. Since
is also connected. Since 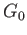 is a
component, we have
is a
component, we have
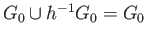 which implies
which implies
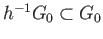 . In particular
. In particular 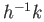 belongs to
belongs to 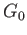 from which we conclude that
from which we conclude that 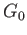 is a subgroup.
is a subgroup.
Interesting properties of topological groups arise in connection with quotients:
nisha
2012-03-20