The group
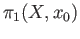 is called the fundamental group of the space X based at
is called the fundamental group of the space X based at  .
This group can be non-abelian although we need to do some work to produce an example.
Indeed we need to do some work to produce such an example for which
.
This group can be non-abelian although we need to do some work to produce an example.
Indeed we need to do some work to produce such an example for which
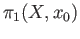 is non-trivial. All we shall
do in the rest of this lecture is to show
that it is trivial in case
is non-trivial. All we shall
do in the rest of this lecture is to show
that it is trivial in case  is a convex subset of
is a convex subset of
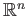 . First we shall see what happens
when the base point is changed.
. First we shall see what happens
when the base point is changed.
nisha
2012-03-20