The set
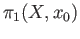 of homotopy classes of loops in
of homotopy classes of loops in  based at
based at  is a group
with respect to the binary operation defined by (7.1). The unit element of the group is the homotopy class of the constant loop at the base point
is a group
with respect to the binary operation defined by (7.1). The unit element of the group is the homotopy class of the constant loop at the base point  and the inverse of
and the inverse of ![$ [\gamma]$](img28.png) is the homotopy class of the loop
is the homotopy class of the loop
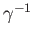 .
.
nisha
2012-03-20