Let  be a path joining
be a path joining
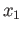 and
and 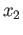 . Observe that if
. Observe that if  is a loop at the
is a loop at the 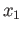 then
then
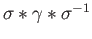 is a loop at
is a loop at 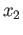 thereby enabling us to define a map
thereby enabling us to define a map
in
Corollary (7.4) shows that the function is well defined and lemma (7.5) shows that it is a group
homomorphism. Let 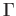 be a loop at
be a loop at 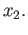 Then
Then
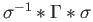 is a loop at
is a loop at 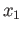 and
and
![$ h_{[\sigma]}([\sigma^{-1} \ast \Gamma \ast \sigma])=[\Gamma]$](img585.png) showing that
showing that
![$ h_{[\sigma]}$](img586.png) is surjective.
The map
is surjective.
The map
is the inverse of
![$ h_{[\sigma]}$](img586.png) .
. 
nisha
2012-03-20