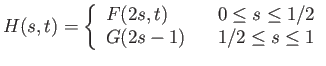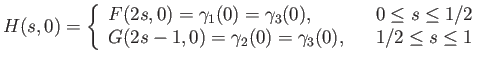It is clear that the homotopy is reflexive, and symmetry is left for student to verify. To prove transitivity
let
![$\displaystyle F:\: [0,1] \times [0,1] \rightarrow X \;\;$](img487.png)
and
![$\displaystyle \;\;
G:\: [0,1] \times [0,1] \rightarrow X
$](img488.png)
be homotopies between the pairs
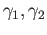 and
and
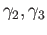 respectively.
Define
respectively.
Define
![$ H : [0,1] \times [0,1] \rightarrow X $](img491.png) by the prescription:
by the prescription:
Note that by gluing lemma  is continuous. We need to check the conditions at endpoints.
is continuous. We need to check the conditions at endpoints.
Likewise one verifies easily
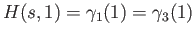 for all
for all
![$ s\in [0,1]$](img478.png) .
Finally we see that
.
Finally we see that
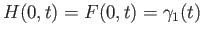 and
and
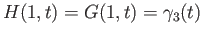 ,
which proves the result.
,
which proves the result.
nisha
2012-03-20