Suppose
![$ \gamma: [0,1] \rightarrow X$](img532.png) is a path then the inverse path
is a path then the inverse path
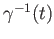 is the path traced in the
reversed direction namely the map
is the path traced in the
reversed direction namely the map
![$ \gamma^{-1} : [0,1] \rightarrow X$](img534.png) given by
given by
The initial point of  is the terminal point of
is the terminal point of
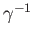 and vice versa.
and vice versa.
The constant path at  is the path
is the path
![$ \varepsilon_{x_0}: [0,1] \longrightarrow X$](img537.png) given by
given by
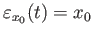
for all
![$\displaystyle t\in [0,1].
$](img539.png)
The following lemma summarizes the main properties of the constant and the inverse paths in terms of the
homotopy classes of paths. Theorem (7.6) spells out the associativity of multiplication of homotopy
classes of paths. The reader would see analogies with the defining properties of a group.
nisha
2012-03-20
![]() is the path
is the path
![]() given by
given by