Suppose
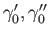 are two paths joining
are two paths joining 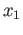 and
and 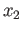 and
and
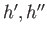 are the corresponding group isomorphisms from
are the corresponding group isomorphisms from
 given by the previous theorem. Then there exists an inner automorphism
given by the previous theorem. Then there exists an inner automorphism
such that
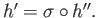 In fact
In fact 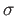 is the inner automorphism determined by
is the inner automorphism determined by
![$ [\gamma_0^\prime][\gamma_0^{\prime \prime}]^{-1}.$](img593.png)
If
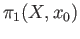 is abelian then
is abelian then
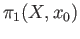 and
and
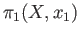 are naturally isomorphic. That is the isomorphism
are naturally isomorphic. That is the isomorphism
![$ h_{[\sigma]}$](img586.png) is canonical in this case.
is canonical in this case.
nisha
2012-03-20
![]() is abelian then
is abelian then
![]() and
and
![]() are naturally isomorphic. That is the isomorphism
are naturally isomorphic. That is the isomorphism
![]() is canonical in this case.
is canonical in this case.