By the previous result it is immaterial which point  is chosen as the base point.
Assume that
is chosen as the base point.
Assume that  is star shaped with respect to
is star shaped with respect to 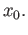 Let
Let
![$ \gamma :[0, 1] \longrightarrow X$](img218.png) be a loop in
be a loop in  based at
based at 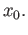 We shall
prove
We shall
prove
![$ [\gamma]=[\varepsilon_{x_0}]=1$](img605.png) by constructing a homotopy
by constructing a homotopy 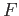 between
between  and
the constant loop
and
the constant loop
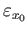 , namely
, namely
This makes sense because  is star shaped with respect to
is star shaped with respect to  . Turning to the boundary conditions,
. Turning to the boundary conditions,
nisha
2012-03-20