- Explicitly construct a homotopy between the loop
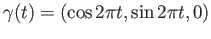 on the sphere
on the sphere 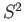 and the constant loop
based at
and the constant loop
based at 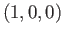 . Note that an explicit formula is being demanded here.
. Note that an explicit formula is being demanded here.
- Show that a loop in
 based at a point
based at a point 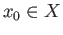 may be regarded as a continuous map
may be regarded as a continuous map
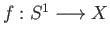 such that
such that
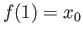 .
Show that if
.
Show that if  is homotopic to the constant loop
is homotopic to the constant loop
 then
then  extends as a continuous map from the closed unit disc to
extends as a continuous map from the closed unit disc to  .
.
- Show that if
 is a path starting at
is a path starting at  and
and
 is the inverse path then prove by imitating the proof of
the reparametrization theorem (that is by taking convex combination of two functions) that
is the inverse path then prove by imitating the proof of
the reparametrization theorem (that is by taking convex combination of two functions) that
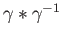 is homotopic to the constant loop
is homotopic to the constant loop
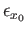 .
.
- Prove theorems (7.2) and theorem (7.6) using Tietze's extension theorem.
- Suppose
![$ \phi : [0, 1] \longrightarrow [0, 1]$](img499.png) is a continuous function such that
is a continuous function such that
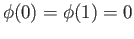 and
and  is a
closed loop in
is a
closed loop in  based at
based at 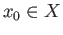 . Is it true that
. Is it true that
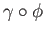 is homotopic to the constant loop
is homotopic to the constant loop
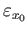 ?
?
- Show that the group isomorphism in theorem (7.8) is natural namely, if
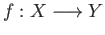 is continuous and
is continuous and
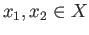 then
then
where,
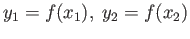 and
and  is a path joining
is a path joining 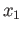 and
and 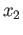 . The maps
. The maps
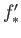 and
and
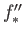 are the maps induced by
are the maps induced by  on the fundamental groups. This information is better
described by saying that the following diagram commutes:
on the fundamental groups. This information is better
described by saying that the following diagram commutes:
in
Lecture VIII - Categories and Functors
Note that one often works with several types of mathematical objects such as groups, abelian groups,
vector spaces and topological spaces. Thus one talks of the family of all groups or the family of all topological spaces.
These entities are huge and do not qualify to be sets. We shall call them families or classes
and their individual members as
objects. Between two objects of a family say between two topological spaces  and
and  one is interested in the class of
all continuous functions. Instead if we take two objects
one is interested in the class of
all continuous functions. Instead if we take two objects  and
and  from the class of all groups we are interested
in the set of all group homomorphisms from
from the class of all groups we are interested
in the set of all group homomorphisms from  into
into  . Abstracting from these examples we say that a category
consists of a family of objects and for each pair of objects
. Abstracting from these examples we say that a category
consists of a family of objects and for each pair of objects  and
and  we are given a family of maps
we are given a family of maps
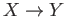 called the set of morphisms
Mor
called the set of morphisms
Mor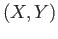 subject to the following properties:
subject to the following properties:
(i) To each pair
Mor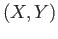 and
Mor
and
Mor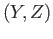 there is a map
there is a map
such that for
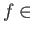 Mor
Mor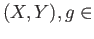 Mor
Mor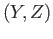 and
and
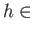 Mor
Mor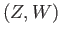 ,
,
(ii) To each object  there is a unique element
id
there is a unique element
id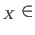 Mor
Mor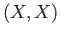 such that for any
such that for any
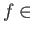 Mor
Mor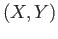 and
and
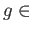 Mor
Mor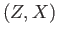
Subsections
nisha
2012-03-20
![$\displaystyle \begin{CD}
\pi_1(X, x_1) @> f_*^{\prime} >> \pi_1(Y, y_1) \\
@...
...gma]}}VV \\
\pi_1(X, x_2) @> f_*^{\prime\prime} >> \pi_1(Y, y_2) \\
\end{CD}$](img623.png)
![]() and
Mor
and
Mor![]() there is a map
there is a map
![]() there is a unique element
id
there is a unique element
id![]() Mor
Mor![]() such that for any
such that for any
![]() Mor
Mor![]() and
and
![]() Mor
Mor![]()