Here we give an example of a contra-variant functor.
The family of all real vector spaces, denoted by
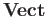 is a category and for a pair of real vector spaces
is a category and for a pair of real vector spaces
 and
and 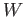 , the set
Mor
, the set
Mor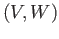 consists of all linear transformations from
consists of all linear transformations from  to
to 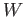 . We define a functor
from
. We define a functor
from
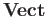 to itself by assigning to each
to itself by assigning to each  its dual
its dual 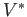 and to each
and to each
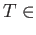 Mor
Mor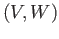 the adjoint map
the adjoint map 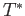 . Again,
. Again,
But if 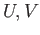 and
and 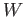 are three vector spaces and
are three vector spaces and
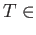 Mor
Mor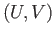 and
and
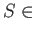 Mor
Mor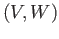 are two
linear maps then
are two
linear maps then
Let us look at an example of a functor from the category of topological spaces to the category
Rng
of commutative rings. We shall always assume that every ring that we shall deal with, has a unit element.
nisha
2012-03-20