Let 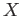 be a topological space and
be a topological space and 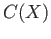 be the set of all continuous functions from
be the set of all continuous functions from
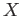 to the real line (with its usual topology). Then
to the real line (with its usual topology). Then 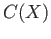 is a commutative ring with unity. Suppose that
is a commutative ring with unity. Suppose that
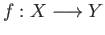 is a continuous map between topological spaces then we define
is a continuous map between topological spaces then we define 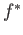 to be the map
to be the map
It is obvious to see that 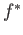 is a ring homomorphism and
id
is a ring homomorphism and
id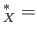 id
id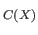 . Further,
. Further,
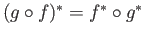 for
for
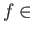 Mor
Mor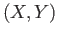 and
and
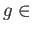 Mor
Mor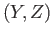 .
We thus have a contravariant functor
Top
.
We thus have a contravariant functor
Top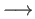 Rng sending the object
Rng sending the object
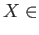 Top to the object
Top to the object
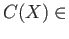 Rng and assigning to
Rng and assigning to
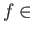 Mor
Mor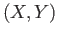 the ring homomorphism
the ring homomorphism
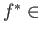 Mor
Mor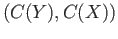 .
.
nisha
2012-03-20