A contravariant functor between the two given categories
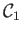 and
and
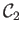 is a rule
that assigns to each object
is a rule
that assigns to each object
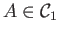 an object
an object
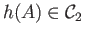 and to each morphism
and to each morphism
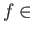 Mor
Mor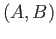 , where
, where 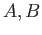 are objects in
are objects in
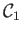 , a unique morphism
, a unique morphism
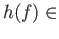 Mor
Mor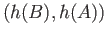 such that the following conditions hold:
such that the following conditions hold:
- (i)
- Given objects
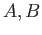 and
and 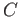 in
in
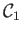 and a pair of morphisms
and a pair of morphisms
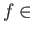 Mor
Mor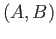 ,
,
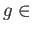 Mor
Mor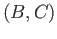 ,
,
- (ii)
-
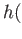 id
id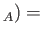 id
id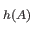
nisha
2012-03-20