Example 8.2:

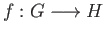To each group $G$ we assign its commutator subgroup $[G, G]$. A group homomorphism $f:G\longrightarrow H$ maps the commutator subgroup into the commutator subgroup $[H, H]$ so that the restriction

$$f\Big\vert _{[G, G]}\;:\;[G, G]\longrightarrow [H, H]$$

is a meaningful group homomorphism enabling us to assign to the morphism $f$ its restriction to $[G, G]$. The conditions of definition 8.1 are readily verified.