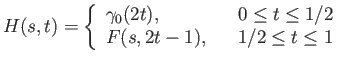Let
![$ F:\: [0,1] \times [0,1] \rightarrow X$](img521.png) be a homotopy between
be a homotopy between
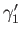 and
and
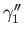 so that
so that
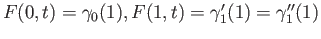 . The homotopy we seek is the map
. The homotopy we seek is the map 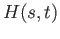 given by
given by
It can be checked that the definition is meaningful along
![$ [0,1] \times \{ \frac{1}{2} \}$](img525.png) and the continuity of
and the continuity of  follows by the gluing lemma. The reader may complete the proof by verifying that
follows by the gluing lemma. The reader may complete the proof by verifying that
nisha
2012-03-20