- Check that the map
 constructed in the proof of theorem 11.3 is continuous and is indeed a homotopy. Work out the proof of theorem 11.5.
constructed in the proof of theorem 11.3 is continuous and is indeed a homotopy. Work out the proof of theorem 11.5.
- Show that the boundary
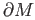 of the Möbius band
of the Möbius band 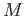 is not a deformation retract of
is not a deformation retract of 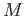 by
taking a base point
by
taking a base point  on the boundary and computing explicitly the
group homomorphism
on the boundary and computing explicitly the
group homomorphism
- Show that the boundary of the Möbius band is not even a retract of the Möbius band.
- Fill in the details on the continuity of the map
 in the example preceding corollary 11.9.
in the example preceding corollary 11.9.
- Show that the space
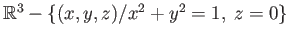 deformation retracts to a sphere with a diameter attached to it.
deformation retracts to a sphere with a diameter attached to it.
- Let
 be the union of
be the union of 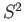 and one of its diameters
and one of its diameters 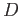 ,
,
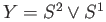 and
and 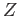 be the union of
be the union of 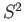 with a punctured half disc contained in a half with edge along
with a punctured half disc contained in a half with edge along 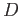 . Show that
. Show that  and
and  are both deformation retracts
of
are both deformation retracts
of 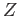 and so they have the same homotopy type.
and so they have the same homotopy type.
in
Lectures XII - XIII The fundamental group of the circle.
in
We have already stated the fact that the fundamental group of the circle is the group of integers and derived some
important consequences form it. The importance of this result
is attested by the fact that the Brouwer's fixed point theorem
for a disc follows immediately from it. In this lecture will provide a detailed proof that
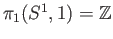 .
Some of the ideas of the proof would appear again later in a general context of covering spaces.
Though this result is a special one from the theory of covering spaces it is worthwhile looking at this
important special case without reference to the general theory but rather as a preview to it. This topic will be
covered in two lectures but the numbering will be as that of lecture 12.
We begin with an algebraic lemma [14] (p. [//]).
.
Some of the ideas of the proof would appear again later in a general context of covering spaces.
Though this result is a special one from the theory of covering spaces it is worthwhile looking at this
important special case without reference to the general theory but rather as a preview to it. This topic will be
covered in two lectures but the numbering will be as that of lecture 12.
We begin with an algebraic lemma [14] (p. [//]).
Subsections
nisha
2012-03-20