The properties of the exponential function used here must be established using power series expansions.
Specifically prove using power series the following:
- (i)
-
ex
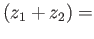 ex
ex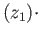 ex
ex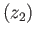
- (ii)
- There exists a unique positive real root of
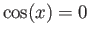 in
in ![$ [0,2]$](img1052.png) (via the real power series for the cosine function) and we denote this root by
(via the real power series for the cosine function) and we denote this root by 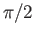 .
.
- (iii)
-
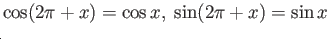 (using addition formula for
(using addition formula for 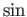 and
and 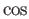 following (i) )
following (i) )
- (iv)
- If
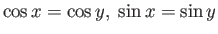 then there exists
then there exists
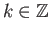 such that
such that
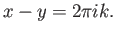
nisha
2012-03-20