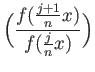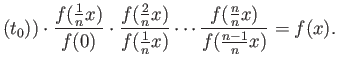Invoking the uniform continuity of  with
with
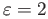 , there
exists
, there
exists
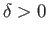 such that
such that
which in turn implies that
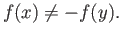 Now choose
Now choose
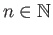 such that
such that
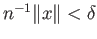 for all
for all 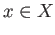 which is possible since
which is possible since  is compact. This
is compact. This  is now fixed for the rest of the discussion.
For
is now fixed for the rest of the discussion.
For 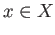 and
and
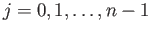
whereby,
From this we conclude that the function given by
lg
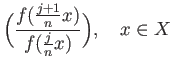
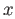 . We now claim that
. We now claim that
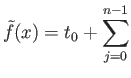
lg
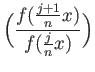
is the required continuous function.
Observe that
lg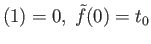 and
and
ex
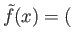
ex
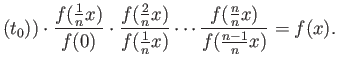
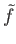 ,
suppose
,
suppose
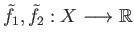 are two continuous functions such that
are two continuous functions such that
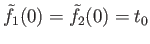 and
ex
and
ex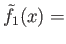 ex
ex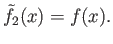 Then
ex
Then
ex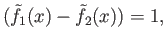 which implies
which implies
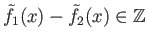 (see note below).
Since both functions are continuous, agree at the origin and
(see note below).
Since both functions are continuous, agree at the origin and  is connected, we conclude that
is connected, we conclude that
nisha
2012-03-20
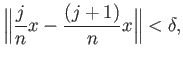
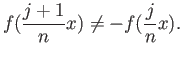
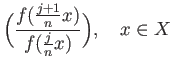
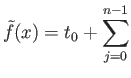 lg
lg