Let  be a compact subset of
be a compact subset of
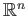 that is star shaped with respect to origin.
Let
that is star shaped with respect to origin.
Let
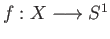 be a continuous function such that
be a continuous function such that
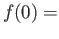 ex
ex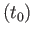 for some
for some
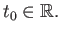 Then, there exists a continuous function
Then, there exists a continuous function
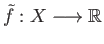 such that
such that
ex
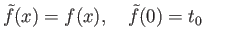
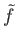 satisfying (12.3) is unique and is called the lift of
satisfying (12.3) is unique and is called the lift of  with respect to ex.
with respect to ex.
nisha
2012-03-20