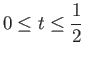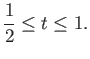Let 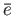 denote the homotopy class of the constant loop based at
denote the homotopy class of the constant loop based at 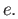 We
first show that the operation
We
first show that the operation 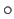 is well defined.
If
is well defined.
If
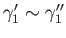 and
and
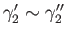 via the respective homotopies
via the respective homotopies
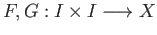 , it is easily checked that the map
, it is easily checked that the map
![$ F \cdot G : [0, 1]\times [0, 1]\longrightarrow X$](img996.png) given by
given by
the product on the right denoting with group multiplication in  ,
is a homotopy between
,
is a homotopy between
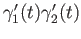 and
and
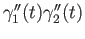 . We conclude that
. We conclude that 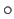 is a well defined binary operation
on
is a well defined binary operation
on
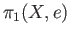 with a two sided unit
with a two sided unit 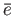 .
Clearly,
.
Clearly, 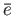 is a common two sided unit element for both binary operations on
is a common two sided unit element for both binary operations on
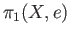 .
To invoke the lemma we show that the two binary operations are mutually distributive.
Let
.
To invoke the lemma we show that the two binary operations are mutually distributive.
Let
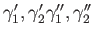 be
loops based at
be
loops based at 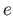
We first verify through direct calculation that
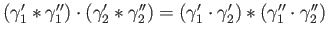 . Well,
. Well,
So finally
Thus lemma (12.1) is applicable for the binary operations 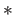 and
and 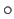 and the proof is complete.
nisha
2012-03-20
and the proof is complete.
nisha
2012-03-20