If X is a topological group with unit element 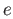 then
then
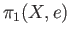 is abelian.
Moreover, if
is abelian.
Moreover, if
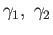 are two loops based at
are two loops based at 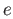 define the binary
operation
define the binary
operation 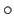 on
on
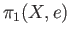 by3
by3
where
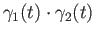 denotes the group multiplication in
denotes the group multiplication in 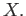 Then
Then
the right hand side being the product in
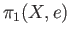 . In other words,
. In other words,
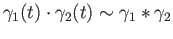 .
.
nisha
2012-03-20