- ... points1
- These are the common zeros of
the pair
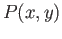 and
and 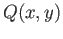 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... equation2
- This means a trajectory
(solution curve) starting at a point of
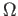 stays in
stays in 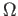 for all times.
for all times.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... by3
- To avoid introducing more notation
we are being notationally imprecise. The expression
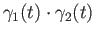 inside the brackets
refers to the map
inside the brackets
refers to the map
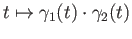 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
covering4
-
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... path5
- The path would have to satisfy some regularity condition such as being
piecewise continuously differentiable. However since this is merely supposed to be a motivation we shall brush
aside these technicalities.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
calculus6
-
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Dieck7
- See also R. Stöcher and H. Zeischang,
Algebraische Topologie,
B. G. Teubner, Stuttgart (1988) 306-325.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.