Lemma 12.1:

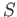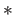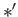Suppose $S$ is a set on which two binary operations $\ast$ and $\ast^\prime$ are defined such that

(a)

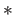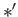Both $\ast$ and $\ast^\prime$ have a common two sided unit.

(b)

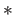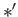The binary operations $\ast$ and $\ast^\prime$ are mutually distributive. That is,

$$(f_1 \ast g_1) \ast^\prime (f_2 \ast g_2) = (f_1 \ast^\prime f_2) \ast (g_1 \ast^\prime g_2), \quad f_1,\;f_2,\;g_1,\;g_2 \in S.$$

Then,

(i)

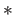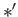both $\ast$ and $\ast^\prime$ are associative and commutative.

(ii)

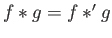$f \ast g= f \ast^\prime g$ for all $f,g \in S.$