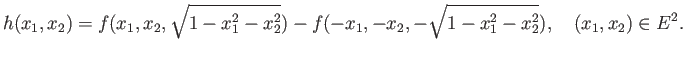We follow the elegant proof given in [17] (p. 109).
We first show that any continuous function
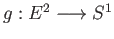 maps a pair of antipodal points on the
boundary of
maps a pair of antipodal points on the
boundary of  to the same point. That is there exists
to the same point. That is there exists  such that
such that 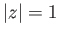 and
and
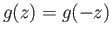 .
Since
.
Since 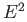 is
a compact convex set, by lemma (12.4) we see that any continuous map
is
a compact convex set, by lemma (12.4) we see that any continuous map
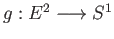 has a continuous lift
has a continuous lift
 . Since the
real valued map
. Since the
real valued map
changes sign we see that there is a pair of antipodal points
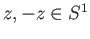 such that
such that
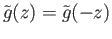 and hence
and hence
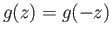 . Turning now to a continuous
map
. Turning now to a continuous
map
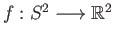 , assume
, assume
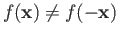 for every
for every
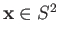 .
We construct the continuous function
.
We construct the continuous function
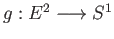
where
Since
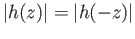 ,
we infer that there is no
,
we infer that there is no 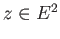 satisfying
satisfying 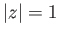 and
and
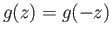 resulting in a contradiction.
resulting in a contradiction.
nisha
2012-03-20