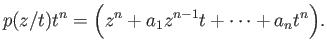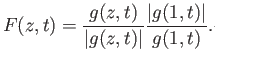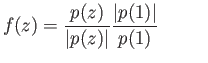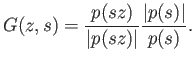If the polynomial
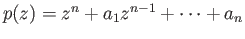 has no zeros, then in particular,
has no zeros, then in particular,
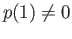 . For
. For 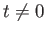 , we define
, we define
The right hand side makes sense even when 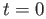 and we denote the right hand side by
and we denote the right hand side by 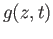 . Observe that
. Observe that
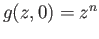 and
and
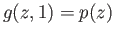 . However we need a homotopy of maps of
. However we need a homotopy of maps of  preserving the base point
preserving the base point 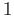 .
To this end we modify it consider instead the map
.
To this end we modify it consider instead the map
![$ F:S^1\times [0, 1]\longrightarrow S^1$](img1173.png) given by
given by
Clearly
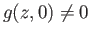 for any
for any 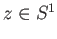 and if
and if
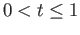 then again
then again
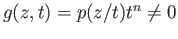 . Thus
(12.7) is a base point preserving homotopy between
the function
. Thus
(12.7) is a base point preserving homotopy between
the function
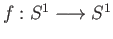 given by
given by
and the map
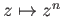 . We conclude that degree of
. We conclude that degree of  is
is  . However we have a base point preserving homotopy
between (12.8) and the constant map namely,
. However we have a base point preserving homotopy
between (12.8) and the constant map namely,
![$ G:S^1\times [0, 1]\longrightarrow S^1$](img1181.png) given by
given by
We now conclude that degree of (12.8) is zero and we have a contradiction.
nisha
2012-03-20