- Formulate and prove the Borsuk Ulam theorem for continuous maps from
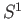 to the real line.
to the real line.
- Use the Borsuk Ulam theorem to prove that a pair of homogeneous polynomials of odd degree in three real variables
have a common non-trivial zero.
- For the following three maps
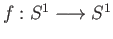 compute the induced map
compute the induced map
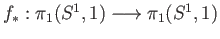 .
All three maps preserve the base point
.
All three maps preserve the base point 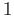 .
.
- (i)
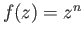
- (ii)
-
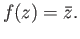
- (iii)
-
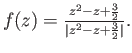 Hint: Is
Hint: Is
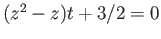 for any
for any 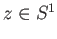 and
and
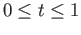 ?
?
- Let
 be the union of the sphere
be the union of the sphere 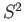 and one of its diameters. Use exercise 1 of lecture 8 to determine
a generator for
and one of its diameters. Use exercise 1 of lecture 8 to determine
a generator for
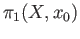 , where
, where  is a point on the sphere.
is a point on the sphere.
- Determine the generators of the group
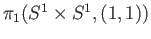 . Determine the generators for the fundamental
group of the space
. Determine the generators for the fundamental
group of the space  of example 11.3.
of example 11.3.
- Compute
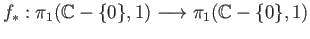 for the function
for the function
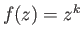 .
.
in
Lecture XIV (Test - II)
in
- Suppose
 is a metric space and
is a metric space and  is a retract of
is a retract of  . Show that
. Show that  is closed in
is closed in  . Is the space homeomorphic to the
letter
. Is the space homeomorphic to the
letter  a deformation retract of a space homeomorphic to
a deformation retract of a space homeomorphic to 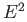 ?
?
- Show that if
 has the fixed point property and
has the fixed point property and  is a retract of
is a retract of  then
then  also has the fixed point property.
also has the fixed point property.
- Find the degree of the following maps
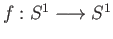 given by:
given by:
- (i)
-
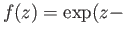 Re
Re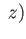 . (ii)
. (ii)
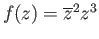 .
.
- Show that
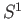 is not homeomorphic to any subset of
is not homeomorphic to any subset of
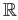 . Can
. Can 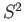 be homeomorphic to a subset of
be homeomorphic to a subset of
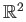 ?
?
- Determine
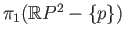 where
where  is any point of
is any point of
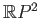 .
.
- For the map
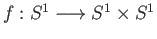 given by
given by
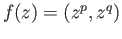 , where
, where  and
and 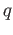 are positive
integers, find the induced group homomorphism
are positive
integers, find the induced group homomorphism
 .
.
in
Lecture XV - Covering Projections
in
The theory of covering projections sets a common stage for the development of diverse branches of mathematics.
In this course we develop the theory of covering projections only to the extent
that is relevant for the computation of the fundamental group. It may be useful for the student to review the proof that
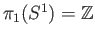 . In fact one of the paradigms for a covering projection is the map
. In fact one of the paradigms for a covering projection is the map
wrapping the real line onto the circle.
Subsections
nisha
2012-03-20
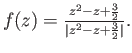 Hint: Is
Hint: Is