Let
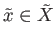 be arbitrary and
be arbitrary and
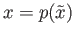 . Choose an evenly covered neighborhood
. Choose an evenly covered neighborhood  of
of 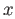 and
and
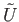 be a sheet lying over
be a sheet lying over  and containing
and containing
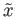 .
Then
.
Then 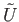 is an open set in
is an open set in
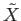 containing
containing
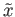 that is
mapped by
that is
mapped by  homeomorphically onto
homeomorphically onto  . Thus
. Thus  is a local homeomorphism and we have proved (i).
Let
is a local homeomorphism and we have proved (i).
Let
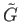 be an arbitrary open set in
be an arbitrary open set in
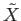 . Then
. Then
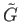 can be covered by open sets
can be covered by open sets
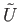 such that
such that  maps each
maps each
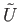 homeomorphically onto an evenly covered
open subset
homeomorphically onto an evenly covered
open subset  of
of  (why?).
Then
(why?).
Then
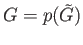 is the union of such evenly covered neighborhoods
is the union of such evenly covered neighborhoods  implying that
implying that  is an open set in
is an open set in  .
Thus
.
Thus  is an open mapping. Finally to prove (iii) suppose that
is an open mapping. Finally to prove (iii) suppose that
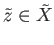 is a limit point of
is a limit point of 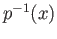 . Pick an arbitrary evenly covered neighborhood
. Pick an arbitrary evenly covered neighborhood  of
of
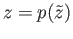 and a sheet
and a sheet
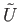 lying over
lying over  containing
containing
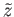 . In particular the restriction of
. In particular the restriction of  to the sheet
to the sheet
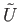 is injective. But since
is injective. But since
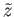 is a limit point of
is a limit point of 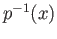 ,
this sheet must contain infinitely many points of
,
this sheet must contain infinitely many points of 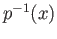 which means
which means  restricted to
restricted to
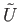 cannot be injective which is a contradiction.
nisha
2012-03-20
cannot be injective which is a contradiction.
nisha
2012-03-20