We now present four examples to illustrate the concept of a covering projection.
- As indicated in the beginning the most basic example is the map
ex
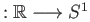 given by
given by
ex
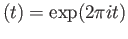
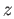 on the circle take an arc
on the circle take an arc  centered at
centered at 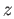 and of length say
and of length say 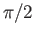 . The reader may
check that the inverse image of
. The reader may
check that the inverse image of  under ex is a disjoint union of open intervals on the line.
under ex is a disjoint union of open intervals on the line.
- Consider the map
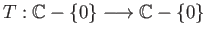 given by
given by
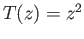 .
If we pick a point
.
If we pick a point
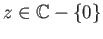 and a small disc
and a small disc  centered at
centered at 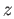 not containing a pair of antipodal points
then
not containing a pair of antipodal points
then 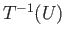 is a disjoint union of two open sets each of which is mapped bijectively onto
is a disjoint union of two open sets each of which is mapped bijectively onto  by
by 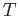 .
.
- Consider the map
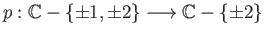 given by
given by
The equation 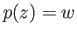 has three distinct roots for each
has three distinct roots for each
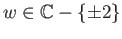 and
the roots are continuous functions of
and
the roots are continuous functions of 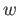 . For a sufficiently small neighborhood
. For a sufficiently small neighborhood  of
of 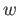 ,
, 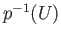 is a
disjoint union of three open sets each of which is mapped onto
is a
disjoint union of three open sets each of which is mapped onto  homeomorphically onto
homeomorphically onto  by the
open mapping theorem. Several examples of this type related to complex analysis are discussed
in [6].
by the
open mapping theorem. Several examples of this type related to complex analysis are discussed
in [6].
- Consider the quotient map
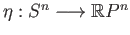 .
We show that
.
We show that 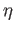 is a covering projection. Let
is a covering projection. Let 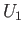 be an
open subset of
be an
open subset of  not containing a pair of anti-podal points and
not containing a pair of anti-podal points and
Then,
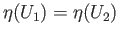 . Denoting these images by
. Denoting these images by  , we see that
, we see that
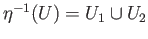 which is an open set in
which is an open set in  and so
and so  is open in
is open in
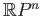 .
Second,
.
Second, 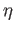 maps each of
maps each of 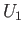 and
and 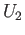 bijectively onto
bijectively onto  . To see that
. To see that 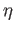 maps
each of
maps
each of 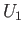 and
and 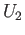 homeomorphically onto
homeomorphically onto  , we merely have to show that
, we merely have to show that 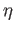 is an open mapping. So let
is an open mapping. So let 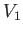 be an open subset of
be an open subset of 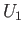 and
and
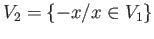 . Then
. Then
is open in  so that
so that 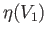 is an open subset of
is an open subset of
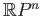 . Thus we have shown that
. Thus we have shown that 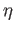 restricted to each
restricted to each 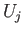 is an open mapping and that suffices for a proof.
is an open mapping and that suffices for a proof.
We now summarize the most basic properties of covering projections.
nisha
2012-03-20