Let  be the subset given by
be the subset given by
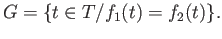 The set
The set  is non-empty since
is non-empty since 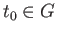 .
We shall show that
.
We shall show that  is both open and closed in
is both open and closed in 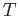 from which the result would follow since
from which the result would follow since 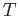 is connected.
For
is connected.
For 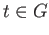 pick an evenly covered neighborhood
pick an evenly covered neighborhood  of
of
and
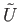 be the sheet lying over
be the sheet lying over  and containing
and containing
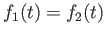 . The set
. The set
is open and contains 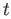 . If
. If 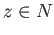 then
then 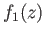 and
and 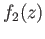 both belong to
both belong to 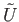 and
and
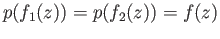 . But
. But  restricted to
restricted to
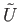 is injective and so
is injective and so
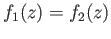 for all
for all 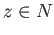 and we conclude that
and we conclude that
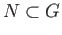 . The proof that
. The proof that  is closed
is left as an exercise. The student may assume that the spaces involved are Hausdorff
(see exercise 7 of lecture 2).
is closed
is left as an exercise. The student may assume that the spaces involved are Hausdorff
(see exercise 7 of lecture 2).
nisha
2012-03-20