- Explain why the map
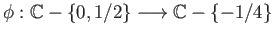 given by
given by
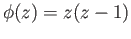 is not a covering projection?
is not a covering projection?
- Show that the map
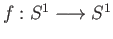 given by
given by
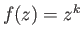 is a covering projection for every
is a covering projection for every
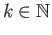 .
.
- Suppose
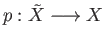 is a covering projection and
is a covering projection and 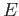 is a closed subset of
is a closed subset of  . Is the map
. Is the map
a covering projection?
- Find a discrete subset
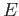 of
of
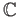 such that
such that
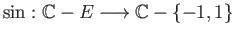 is a covering projection.
is a covering projection.
- Suppose that
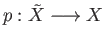 and
and
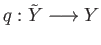 are covering projections then the product map
are covering projections then the product map
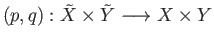 given by
given by
is a covering projection. In particular the plane
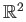 is a covering space of the torus
is a covering space of the torus
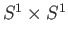 .
.
- Let
 be the infinite grid
be the infinite grid
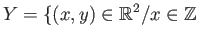
or
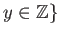
is a covering projection of the figure eight loop. Draw the figure eight loop on the torus.
- Show that the set
 in theorem (15.2) is closed without using the Hausdorff assumption on
in theorem (15.2) is closed without using the Hausdorff assumption on 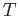 .
.
in
in
Lecture XVI - Lifting of paths and homotopies
In the last lecture we discussed the lifting problem and proved that the lift if it exists is uniquely determined by its value at one point.
In this lecture we shall prove the important result that covering projections enjoy the path lifting and covering homotopy properties. This
theorem is fundamental in the the theory of covering projections and
will be used in the next lecture to define an action of the fundamental group on the fibers.
Subsections
nisha
2012-03-20