Let
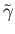 be a loop in
be a loop in
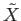 based at
based at
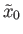 that represents an element of
ker
that represents an element of
ker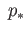 . This means the loop
. This means the loop
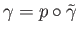 is
homotopic to the constant loop in
is
homotopic to the constant loop in  based at
based at  .
But the constant loop
.
But the constant loop
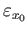 at
at  lifts as the constant loop
lifts as the constant loop
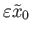 at
at
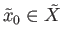 . By the covering homotopy theorem we conclude that
. By the covering homotopy theorem we conclude that
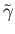 and the constant loop
and the constant loop
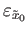 are homotopic. That is to say
are homotopic. That is to say
![$ [\tilde \gamma]$](img1372.png) is the trivial element in
is the trivial element in
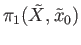 .
. 
nisha
2012-03-20