We shall construct injective maps from
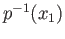 into
into
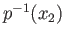 and vice versa. Fix a path
and vice versa. Fix a path 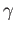 in
in 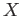 joining
joining 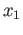 and
and 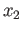 .
Pick
.
Pick
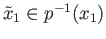 and let
and let
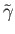 be the lift of
be the lift of 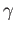 starting at
starting at
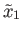 and define a map
and define a map
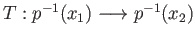 by the prescription
by the prescription
Likewise let
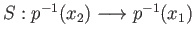 be the map in the reverse direction constructed using the path
be the map in the reverse direction constructed using the path
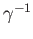 .
Since the inverse path
.
Since the inverse path
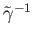 is the unique lift of
is the unique lift of
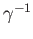 starting at
starting at
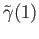 , we see that
, we see that
whereby we conclude 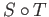 is the identity map on
is the identity map on
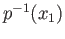 . By symmetry
. By symmetry 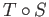 is the identity map on
is the identity map on
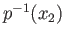 as desired.
as desired. 
nisha
2012-03-20