Let
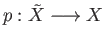 be a covering projection and
be a covering projection and
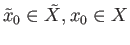 be chosen base points such that
be chosen base points such that
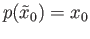 . Let
. Let
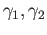 be two
curves in
be two
curves in  starting at
starting at  and having the same terminal points and
and having the same terminal points and
![$ F: [0, 1]\times [0, 1] \longrightarrow X$](img504.png) be a homotopy between
be a homotopy between
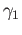 and
and 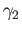 . There is a unique lift
. There is a unique lift
![$ {\tilde F}: [0, 1]\times [0, 1]\longrightarrow {\tilde X}$](img1332.png) of
of 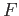 such that
such that
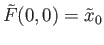 . In particular the unique lifts of
. In particular the unique lifts of 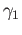 and
and 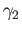 starting at
starting at
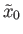 have the same terminal points.
have the same terminal points.
nisha
2012-03-20