The idea behind the proof is
simple and parallels the proof of the previous theorem except that the book-keeping gets a bit more involved.
Consider a covering 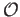 of
of  by evenly covered open neighborhoods and choose a Lebesgue number
by evenly covered open neighborhoods and choose a Lebesgue number
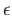 for the covering
for the covering
Choose  so large that any square in
so large that any square in
![$ [0, 1]\times [0, 1]$](img213.png) of side
of side 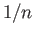 is contained in one of the sets
is contained in one of the sets
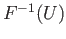 in (16.3). Partition
in (16.3). Partition
![$ [0, 1]\times [0, 1]$](img213.png) using the grid points
using the grid points
and 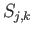 be the square with vertices
be the square with vertices
Figure:
Homotopy lifting property
|
[width=.4]GKSBook/fig13/fig13.eps |
Let 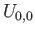 be an evenly covered neighborhood in
be an evenly covered neighborhood in  such that
such that
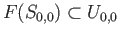 and
and
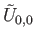 be the sheet in
be the sheet in
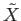 lying above
lying above 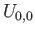 . Denoting by
. Denoting by 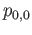 and
and 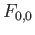 the restrictions of
the restrictions of  and
and 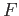 to
to
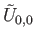 and
and 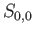 respectively,
define
respectively,
define
Thus
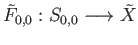 is continuous, takes the value
is continuous, takes the value
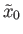 at the origin and is a
part of the lift
at the origin and is a
part of the lift
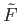 under construction.
As in the previous theorem we shall construct the lift
under construction.
As in the previous theorem we shall construct the lift
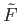 piece by piece and
we now turn to the adjacent square
piece by piece and
we now turn to the adjacent square 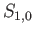 which is mapped by
which is mapped by 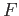 to an evenly covered neighborhood
to an evenly covered neighborhood 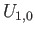 in the cover
in the cover  .
In particular (referring to the figure)
.
In particular (referring to the figure)
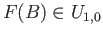 . Choose a sheet
. Choose a sheet
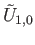 lying above
lying above 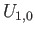 containing
containing
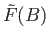 and the restriction
and the restriction
maps
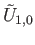 homeomorphically onto
homeomorphically onto 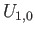 . Now we define the next piece of the lift
. Now we define the next piece of the lift
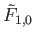 as
as
which is continuous on the square 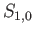 and
and
In order to glue together the pieces
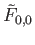 and
and
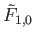 we must ensure that they agree all along the common edge
we must ensure that they agree all along the common edge 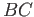 of the adjacent
squares
of the adjacent
squares 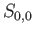 and
and 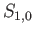 . Their restrictions along
. Their restrictions along 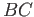 where
where 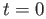 and
and
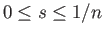 agree at
agree at 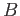 namely
namely
and are both lifts of the map
which implies, by uniqueness of lifts,
as desired. It is now clear how the construction ought to proceed and we get a lift
![$ {\tilde F}: [0, 1]\times [0, 1]\longrightarrow {\tilde X}$](img1332.png) of
of 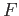 .
.
We now have to check that
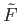 is indeed a homotopy of paths with fixed endpoints. Well,
is indeed a homotopy of paths with fixed endpoints. Well,
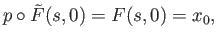
for all
![$\displaystyle s \in [0,1]
$](img1091.png)
so that the connected set
is contained in the discrete set
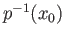 and so must reduce to a singleton. Likewise
and so must reduce to a singleton. Likewise
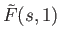 is constant as
is constant as 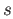 varies over
varies over ![$ [0, 1]$](img13.png) .
Also
.
Also
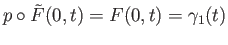 and
and
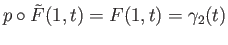 showing that
showing that
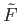 is the desired
homotopy between the lifts of
is the desired
homotopy between the lifts of 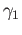 and
and 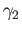 starting at
starting at
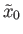 .
.  nisha
2012-03-20
nisha
2012-03-20
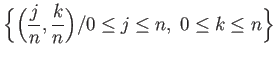
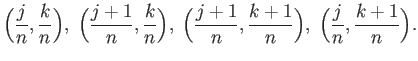
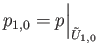
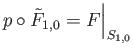
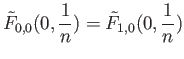
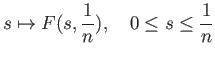
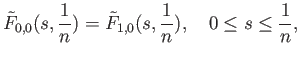
![]() is indeed a homotopy of paths with fixed endpoints. Well,
is indeed a homotopy of paths with fixed endpoints. Well,