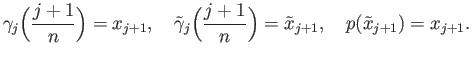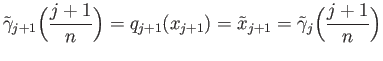Let  be the open cover of
be the open cover of  by evenly covered open sets and
by evenly covered open sets and
 be the family
be the family
of open sets covering ![$ [0, 1]$](img13.png) .
There is a Lebesgue number
.
There is a Lebesgue number 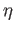 for this cover and we choose
for this cover and we choose  to be a natural number such that
to be a natural number such that
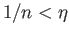 .
Consider the partition
.
Consider the partition
For each
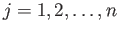 , the piece
, the piece
![$ \gamma([\frac{j-1}{n}, \frac{j}{n}])$](img1296.png) lies in an evenly covered open set in
lies in an evenly covered open set in  . In particular if
. In particular if
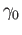 denotes the restriction of
denotes the restriction of  to
to ![$ [0, 1/n]$](img1298.png) then the image of
then the image of 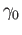 lies in an open set
lies in an open set
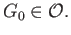 The conditions
(16.1)-(16.2) say that there is a sheet
The conditions
(16.1)-(16.2) say that there is a sheet
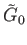 lying over
lying over 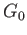 and containing the point
and containing the point
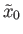 . Let
. Let 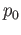 denote the restriction
of
denote the restriction
of  to the sheet
to the sheet
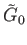 and
and 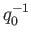 be its inverse. On the sub-interval
be its inverse. On the sub-interval ![$ [0, 1/n]$](img1298.png) , we define
, we define
thereby obtaining an initial piece of the desired lift
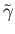 . We shall construct the lift
. We shall construct the lift
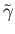 piece by piece defining it on each subinterval of the partition of
piece by piece defining it on each subinterval of the partition of ![$ [0, 1]$](img13.png) .
In what follows
.
In what follows 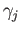 denotes the restriction of
denotes the restriction of
 to the sub-interval
to the sub-interval
![$ [\frac{j}{n}, \frac{j+1}{n}]$](img1305.png) . Assume inductively that
. Assume inductively that
has been defined such that
For the inductive step we set up the notations for the endpoints of the lift
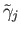 namely,
let
namely,
let
Let
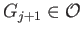 be an evenly covered neighborhood containing
be an evenly covered neighborhood containing 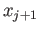 such that
such that  maps
maps
![$ [\frac{j+1}{n}, \frac{j+2}{n}]$](img1318.png) into
into
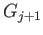 and
and
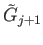 be the sheet lying over
be the sheet lying over
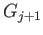 containing the point
containing the point
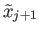 .
The restriction of
.
The restriction of  to
to
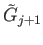 is a homeomorphism with inverse
is a homeomorphism with inverse 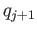 say, so that
say, so that
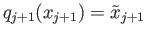 . We set
. We set
Then
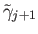 is continuous,
is continuous,
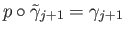 and
and
By gluing lemma, the pieces
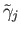 may be glued together to yield a continuous function
may be glued together to yield a continuous function
![$ {\tilde \gamma}: [0, 1] \longrightarrow {\tilde X}$](img1328.png) such that
such that
The proof is complete. The uniqueness has been already proved in general.
nisha
2012-03-20
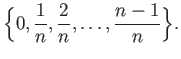
![$\displaystyle {\tilde\gamma}_j:[\frac{j}{n}, \frac{j+1}{n}] \longrightarrow {\tilde X}
$](img1306.png)