A covering projection is a triple
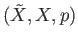 where
where 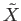 ,
,  are
connected topological spaces and a continuous map
are
connected topological spaces and a continuous map
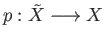 satisfying the following
properties:
satisfying the following
properties:
- (i)
- The map
 is surjective
is surjective
- (ii)
- Each
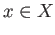 has a neighborhood
has a neighborhood  such that the inverse image
such that the inverse image 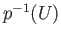 is a disjoint union
of a collection open subsets
is a disjoint union
of a collection open subsets
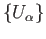 of
of 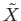 .
.
- (iii)
- Each
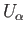 is mapped onto
is mapped onto  homeomorphically by
homeomorphically by  .
.
The neighborhood  described in the definition above is called an
evenly covered neighborhood of
described in the definition above is called an
evenly covered neighborhood of 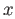 and the open sets
and the open sets
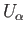 are referred to as sheets
lying above
are referred to as sheets
lying above  .
This terminology will be used
frequently. We shall also say that
.
This terminology will be used
frequently. We shall also say that 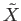 is a covering space of
is a covering space of  when it is fairly clear what the map
when it is fairly clear what the map  is.
in
is.
in
nisha
2012-03-20