Let
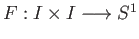 be the homotopy between
be the homotopy between 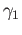 and
and 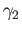 . Since
. Since
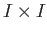 is star shaped with respect to
is star shaped with respect to 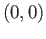 and
and
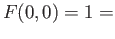 ex
ex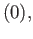 the
lifting lemma gives a unique lift
the
lifting lemma gives a unique lift
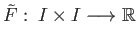 with
with
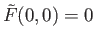 .
The image
.
The image 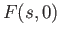 is a connected subset of
is a connected subset of
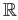 as
as 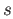 runs from 0 to
runs from 0 to 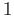 and
exp
and
exp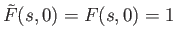 for all
for all
![$ s\in [0,1]$](img478.png) .
So
.
So
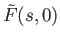 is integer valued and hence constant. From
is integer valued and hence constant. From
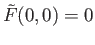 we conclude that
we conclude that
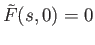 for all
for all
![$ s\in [0,1]$](img478.png) .
In particular the lifts
.
In particular the lifts
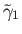 and
and
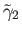 both start at the origin and
so
both start at the origin and
so
deg
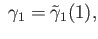
deg
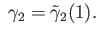
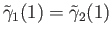 .
Well,
.
Well,
 must map the connected set
must map the connected set
 onto a connected
subset
onto a connected
subset 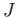 of
of
 and since
and since
ex
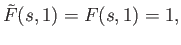
 must be a subset of
must be a subset of
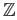 and hence reduces to a singleton which means
and hence reduces to a singleton which means
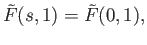
for all
![$\displaystyle s \in [0,1]
$](img1091.png)
Setting 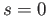 and
and 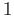 we see that
we see that
thereby completing the proof that the map
![$ \phi:[\gamma] \mapsto$](img1094.png) deg
deg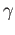 is well defined.
nisha
2012-03-20
is well defined.
nisha
2012-03-20