Proof:

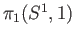Since $[\eta]$ generates $\pi_1(S^1, 1)$, writing the group operation additively, we have

$$f_*[\eta] = c[\eta] \eqno(12.6)$$

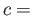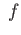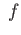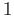We have to show that $c =$   deg$\;f$. By definition, $f_*[\eta] = [f\circ \eta]$ which is mapped to deg$\;f$ by the isomorphism $\phi$ of lemma (12.5). But this isomorphism maps $[\eta]$ to $1$ and hence applying $\phi$ to (12.6) we get the result. $\square$