| |
The proofs of (i) follows obviously from the definition of absolute value.
To prove (ii) we consider different cases. The required property is obvious if both x, y 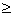 0 . 0 .
In case 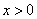 and and 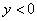 ) , we have ) , we have
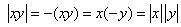
The other cases can be analyzed similarly.
To prove (iii) suppose 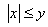 . If . If 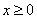 , then , then
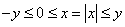
If 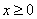 , then , then
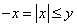
Thus, 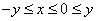
Conversely, let 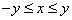 . If . If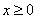 , then , then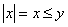 . If . If 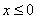 , then , then 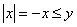 . Thus (iii) holds. . Thus (iii) holds.
To prove (iv), note that
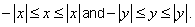
Adding the two we get
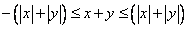
and hence by (iii), 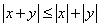 . .
Finally, to prove (v) , note that by (iv)
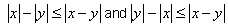 . .
Hence (v) follows from (iii).
 Back Back |